This is a report of sorts of my playing around with OthelloGPT, a GPT model trained on Othello games to predict all the possible legal moves.
It is a common problem in Machine Learning to talk about whether a model is just remembering information, performing surface statistics or is actually doing something deeper? We try to investigate this for OthelloGPT!
The original paper by Kenneth Li et. al. find that this model is not just performing sequence statistics, the model representation infact has a world model of the Othello environment.
The authors make multiple arguments like a) how the world model representation is being used to draw inferences, b) how a non-linear probe can actually input the internal representation of the model and output (with high accuracy!) the current board state and c) how altering the internal representation ends up having the intended effect on the predictions. They also have a more accessible version of it as a blog.
Later Neel Nanda et al publish a paper talking about their findings on how this representation is, well, actually linear! You need to view in a particular direction to find the linearity!
In this project, I dealt with the following problem:
How Does The Model Compute That A Certain Cell is Blank?
This seems like an easy thing to compute, as all you need to do is to figure out whether the \((i,j)^{\text{th}}\) cell has appeared in the move sequence or not.
Goals:
At which layer does the model conclude that it’s blank?
Does this come from any specific head or neuron?
How could a transformer detect this?
We hypothesize that a single attention head per cell is what is used by a transformer. Let’s try to answer these questions one-by-one.
Goal #1 At which layer does the model conclude that it’s blank?
Let us first fix some notation. Let \(X_L\) be the intervention by the linear probe at the \(L\)’th layer of the residual stream. Let \(Y\) be the true representation of the game board.
We try to find its goodness at two things:
Test #1: The prediction is blank
CONDITIONALon the true representation being blankTest #2: The prediction is NOT blank
CONDITIONALon the correct representation being NOT blank
We calculate the following conditional probabilities and plot them (which themselves are tensors of the shape \(\text{rows} \times \text{cols}\)). Ofcourse we only care about the games in the middle because if not, things become a bit more weird.\[ \text{Test 1: }P(X_L = Y \Bigg|Y=\text{Blank}) = \frac{P(X_L = Y \text{ and } Y=\text{Blank})}{P(Y=\text{Blank})} \]
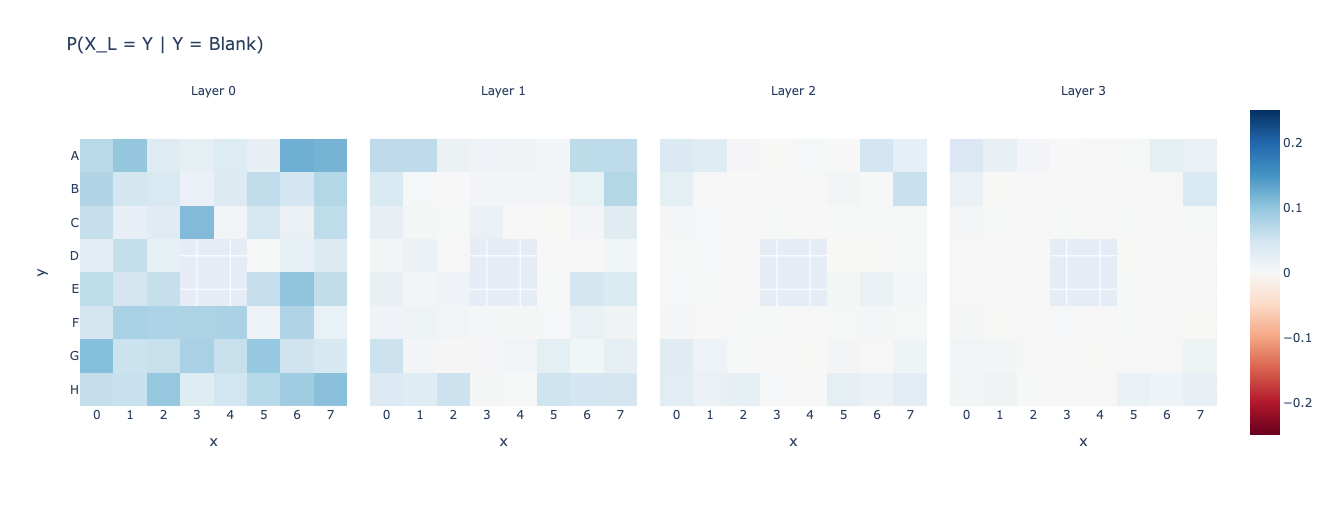
Notice that the 4 squares in the middle have NaN value. This is because those can never be blank and so there’s a division by zero error. It isn’t an issue for us though.
Also, there doesn’t seem to be much improvement after Layer 1, so let us just focus on the first two layers.
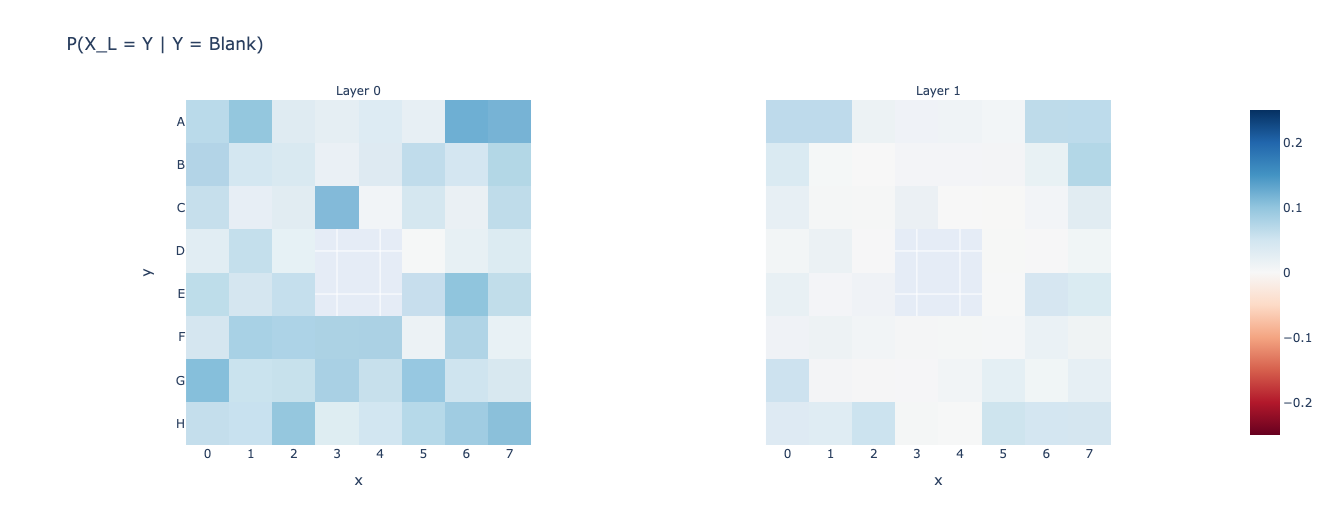
Let’s also find out the \(\text{maxerr}\) and \(\text{avgerr}\) across layers and plot it.
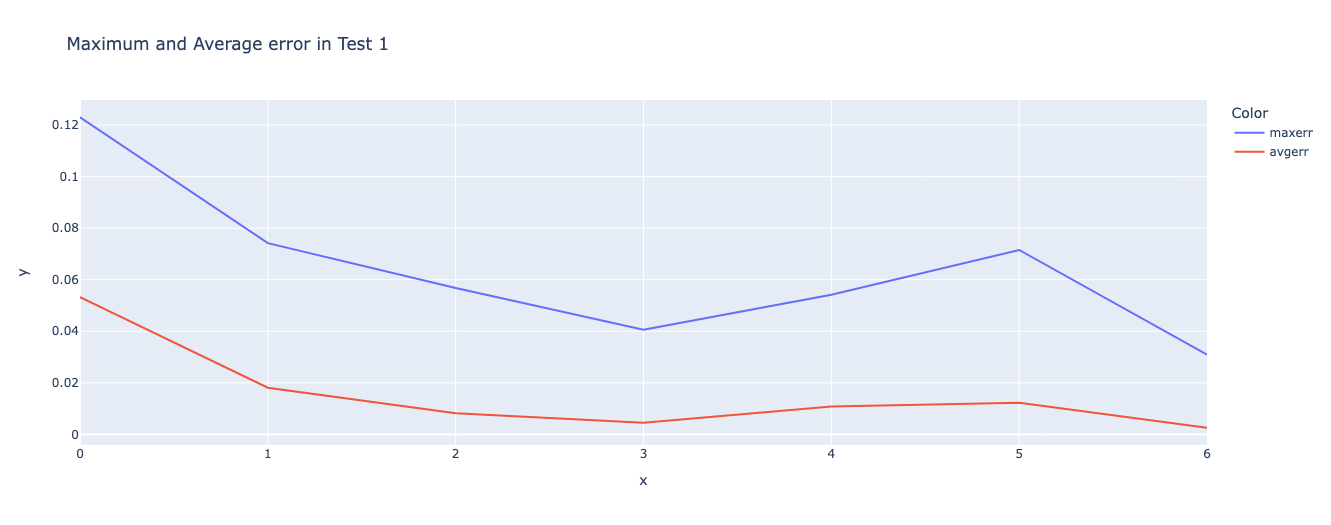
Looking at this plot, it seems like a good idea to hypothesize that most of the Is_Blank computation is done in Layer 0 (for most cells) and some of the remaining computation is done in Layer 1. It seems that Layer 1 is what gives it structure finally, though.
Let’s now do the second test.
\[ \text{Test 2: }P(X_L \neq \text{Blank} \Bigg|Y\neq\text{Blank}) = \frac{P(X_L \neq \text{Blank} \text{ and } Y\neq\text{Blank})}{P(Y\neq\text{Blank})} \]
We calculate and then plot the same graphs.
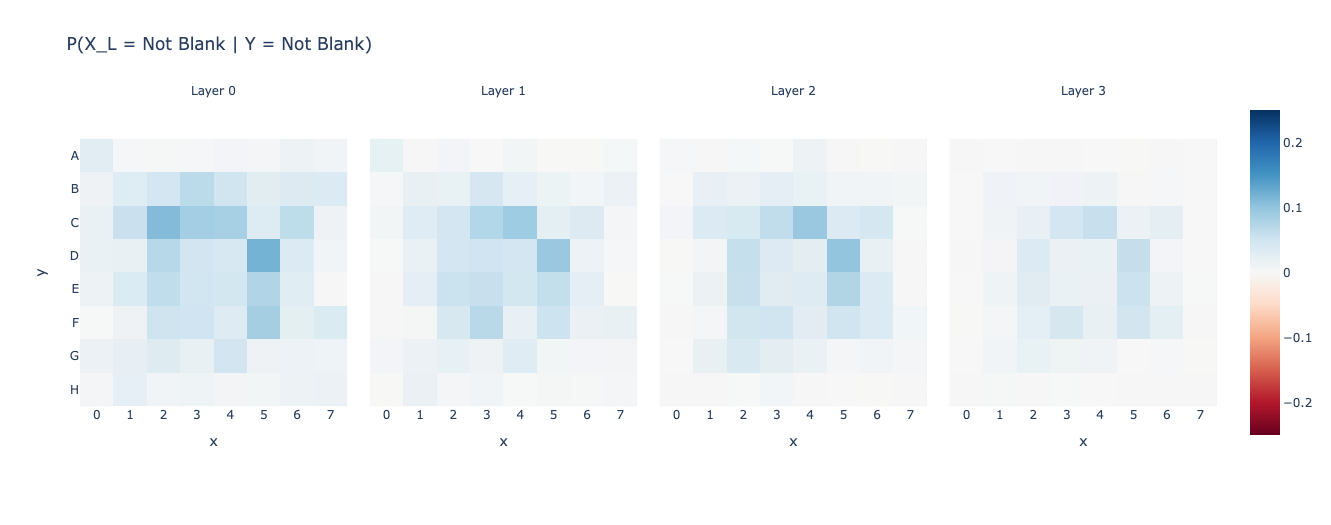
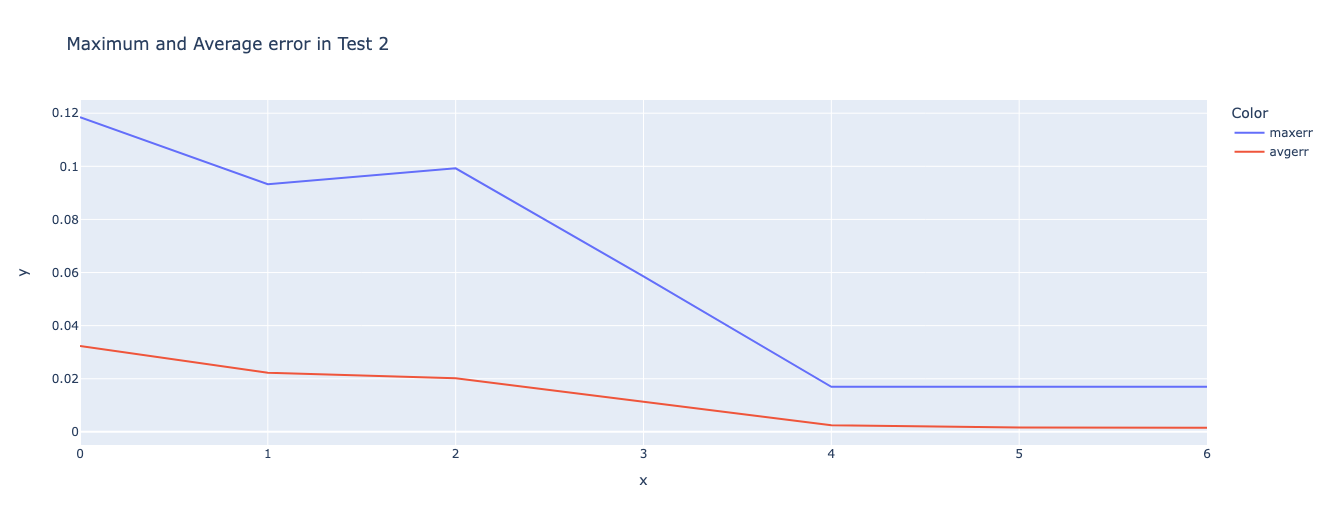
Ah! I thought that the features Is_Blank and Is_Not_Blank would get implemented almost together, and although that does seem to be the case, the \(\text{maxerr}\) only really gets close to the average error by Layer 4, which is precisely where the OthelloGPT has created a high-accuracy world model (according to Neel’s findings). This is all super interesting!
Let us now try to answer a more important question.
Goal #2 Does this come from any specific head or neuron?
Let’s look at the cosine similarity of output weights and the blank colour probe for top layer 0 and layer 1 neurons sorted according to standard deviation (sorting wrt to “resid_post”)
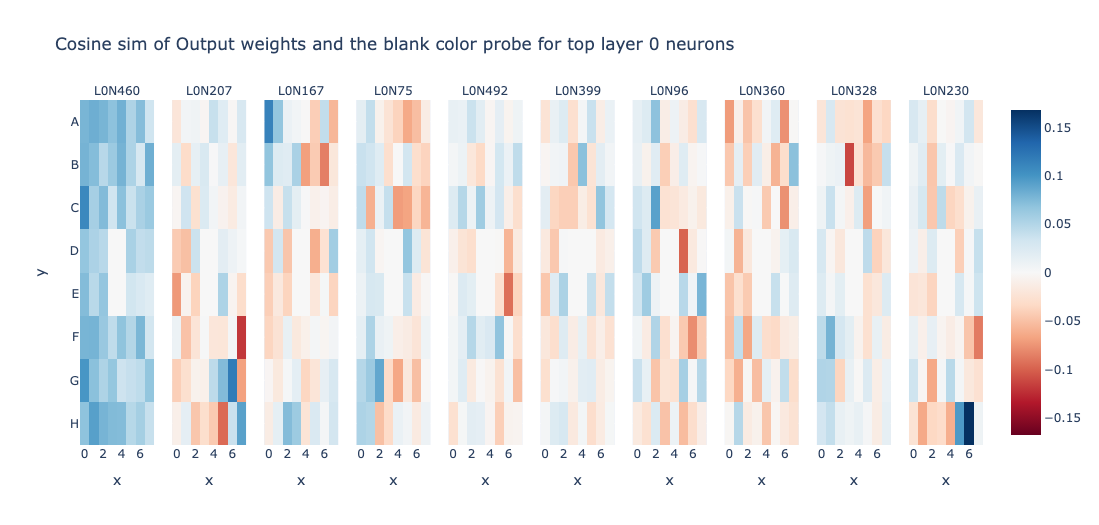
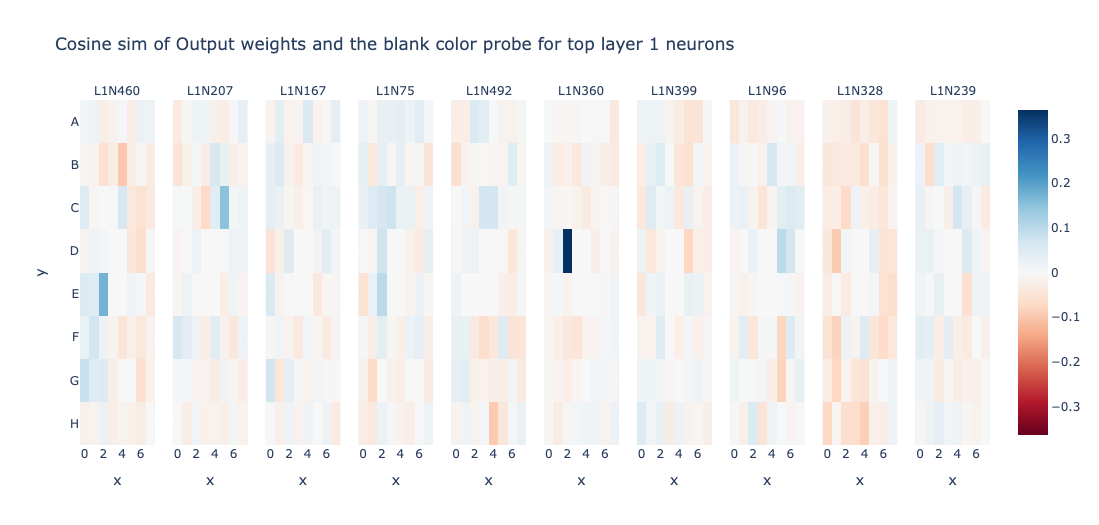
Layer 0 resid_post doesn’t seem very interpretable to me. However, L1N360 looks very interesting. It computes Is_Blank of cell D2. Can we find more such neurons? Let’s try to use the same technique on post
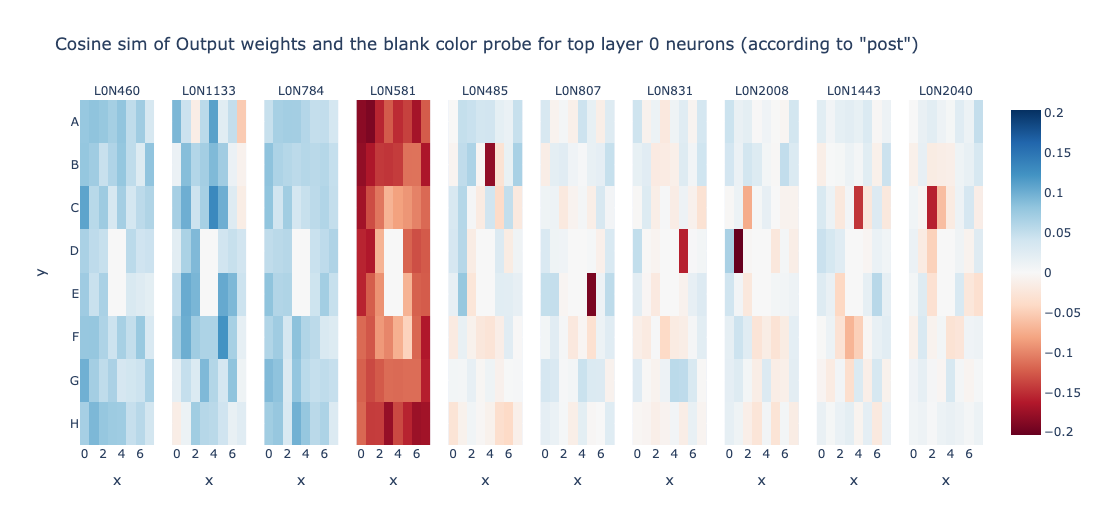
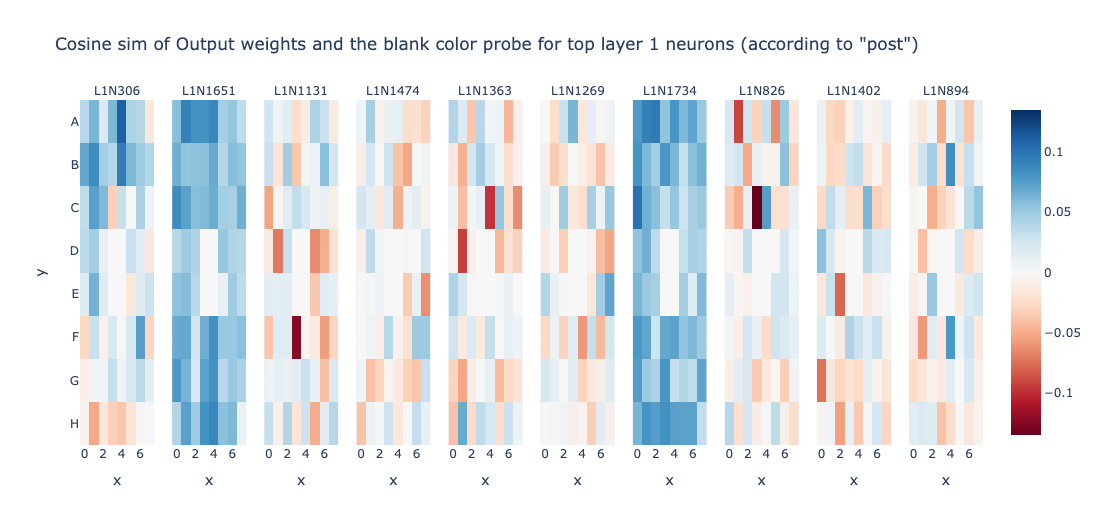
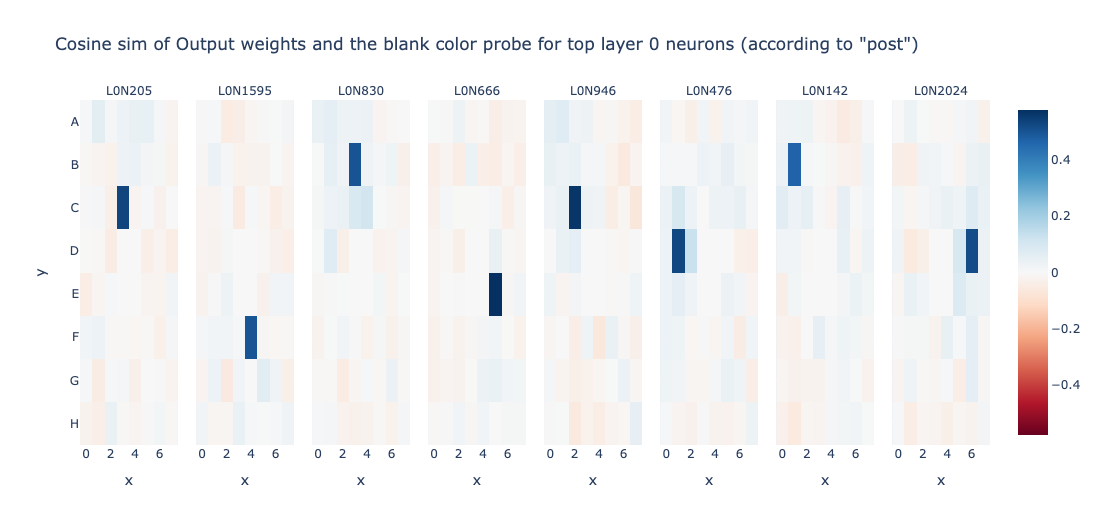
Wow! Layer 0 seems to compute bunch of Not_Is_Blank features for particular cells. Let’s try to find more such neurons!
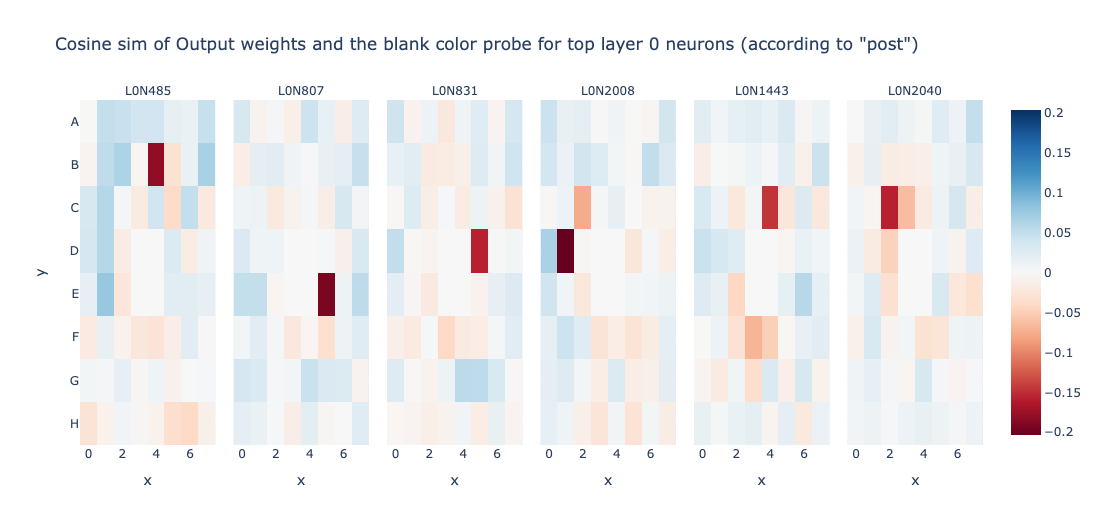
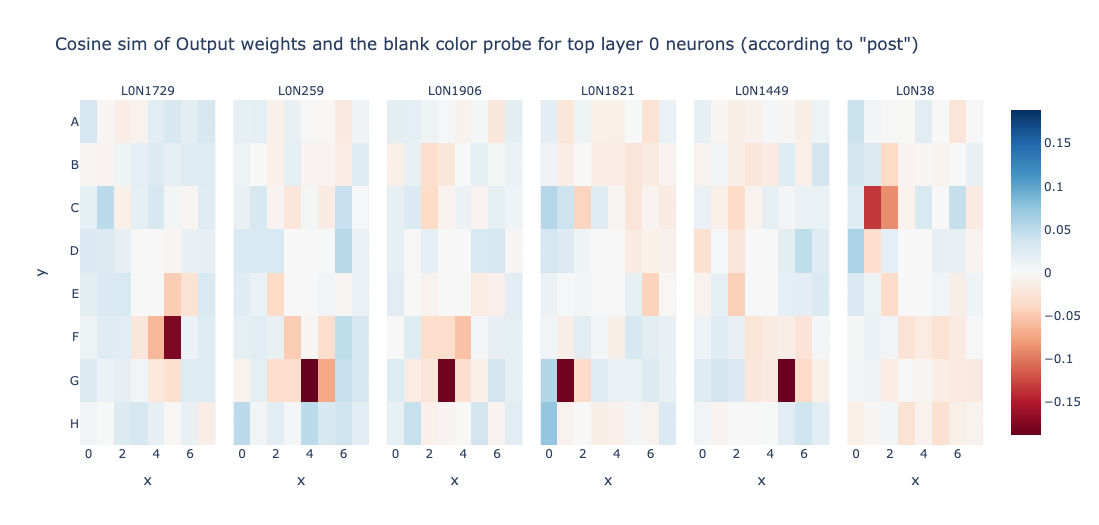
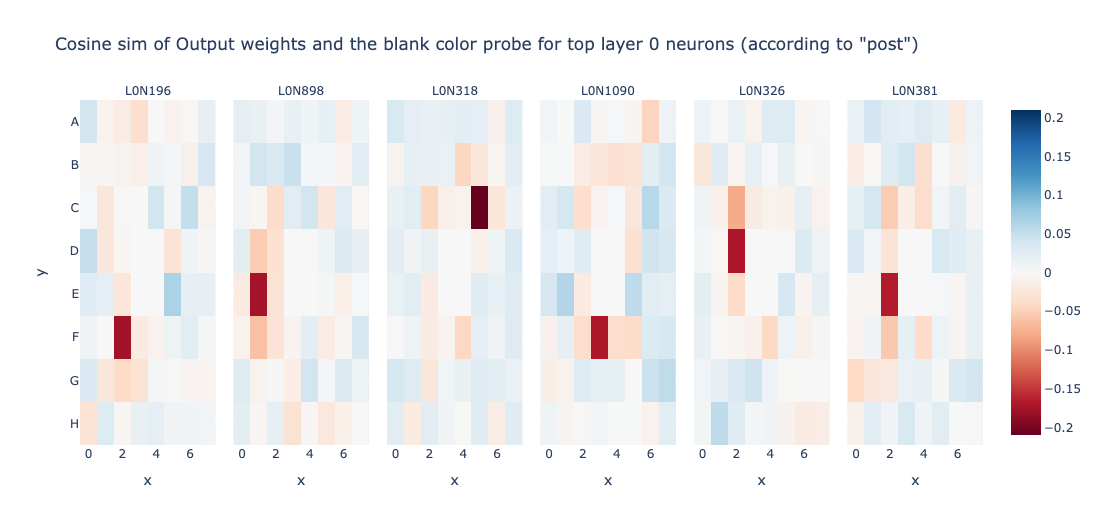
Wait! This is all cool and stuff, but what about Is_Blank features? Is Layer 0 not computing it? Lets try to change the experiment in a way to obtain neurons that track Is_Blank heavily.
I will start with a bound \(M_U\) on the absolute values of the cosine sim, so that anything above \(M_U\) will be treated as \(1\) and anything below \(M_U\) will be treated as 0. Could I find something interesting out of this simple setup?
top_layer_0_neurons = ((focus_cache["post", 0][:, 3:-3]).abs() > Mu).float().std(dim=[0,1]).argsort(descending=True)
Setting \(M_U = 0.2, 0.3, 0.4\) etc give us bunch of neurons that are very highly correlated to the Is_Blank probe for a single cell! This is more evidence for our hypothesis that Layer 0 computes the Is_Blank feature. Infact, this makes it highly interpretable.
Goal #3 How could a transformer come up with this?
WIP!